作为一项国际知名的计算机竞赛,USACO在美国乃至全球范围内享有极高的认可度。它不仅是麻省理工学院等名校推荐的竞赛项目之一,更是想要申请顶尖理工院校的学生的“秘密武器”。USACO是一个为高中生设计的计算机编程竞赛,旨在选拔参加国际信息学奥林匹克竞赛(IOI)的美国国家队队员。
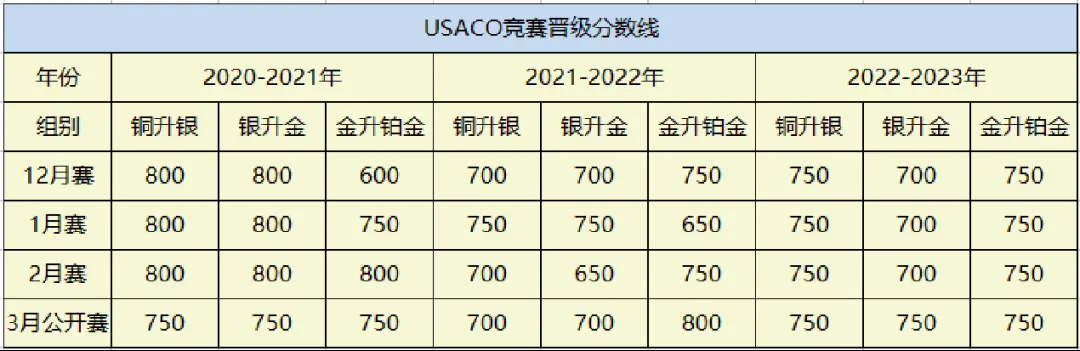
USACO不同等级需要什么参赛基础?
1.铜级(Bronze)
- 需要掌握至少一种编程语言的基础知识(如C++、Java或Python)。
- 理解基本的程序结构,比如条件语句、循环、函数/方法的定义与调用等。
- 能够解决简单的问题,这些问题通常不需要复杂的数据结构或算法。
2.银级(Silver)
- 在铜级的基础上,需要具备更好的问题解决技巧。
- 了解并能使用一些简单的数据结构,例如数组、列表、栈、队列。
- 对于排序算法有一定的理解,并能够实现常见的搜索算法(如二分查找)。
- 能够处理稍微复杂的逻辑和更大型的代码项目。
3.金级(Gold)
- 具备较强的算法背景,包括但不限于图论中的最短路径算法(Dijkstra, Bellman-Ford)、最小生成树(Prim, Kruskal)等。
- 深入理解动态规划的概念及其应用。
- 掌握更多高级数据结构,如平衡二叉搜索树、堆、哈希表等。
- 能够分析问题的时间复杂度和空间复杂度,并选择合适的算法来优化解决方案。
4.铂金级(Platinum)
- 对于算法有非常深入的理解,并且能够在较短时间内开发出高效的算法来解决复杂数学问题。
- 不仅限于标准算法的学习,还需要创造性地思考问题,可能涉及组合数学、数论等领域。
- 可以有效地利用各种数据结构来存储和操作大量数据。
- 具备良好的编码实践和调试能力,以及在高压环境下快速解决问题的能力。
为了准备USACO的比赛,选手们应该多做练习题,阅读相关的书籍资料,并参加在线课程或者工作坊来提升自己的技能。此外,熟悉比赛规则和时间管理也很重要。随着级别的提高,不仅技术难度增加,对参赛者独立思考和创新性解决问题的要求也相应提升。
【扫码免费领取】USACO真题+备赛书单+一对一备考规划!
预约最新真题讲座、课程详情可添加下方顾问老师咨询



思维导图