作为美国的信息学竞赛,USACO在国际竞赛中享有极高的声誉。特别是对于那些希望冲刺海内外计算机专业名校的学生来说,参加USACO竞赛无疑是一项非常有益的举措。通过参与USACO竞赛,你不仅可以锻炼自己的编程能力和算法思维,还可以为自己的申请加分。
USACO竞赛3月公开赛
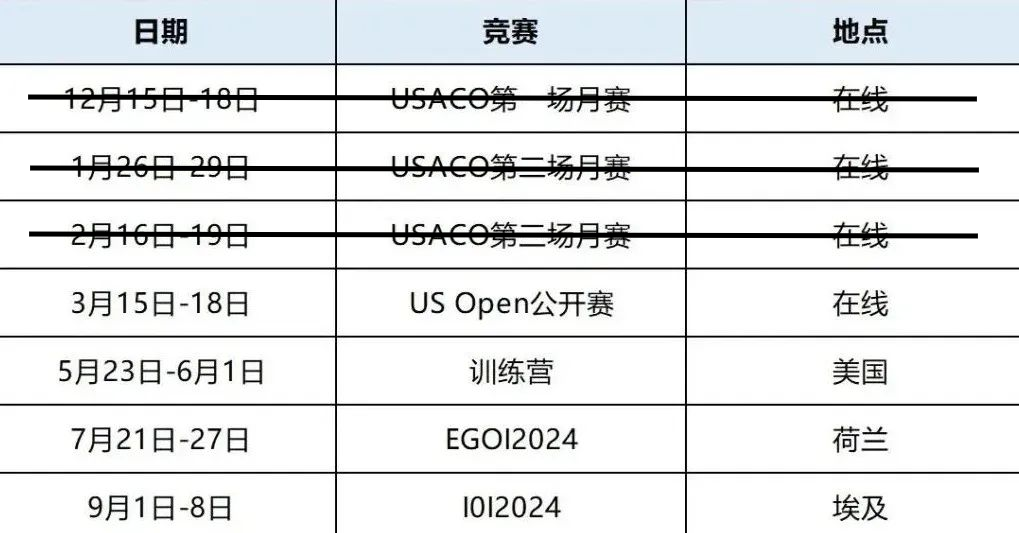
USACO竞赛3月公开赛在2024年3月15日-3月18日,3月公开赛考试时长为5小时,题目会比月赛更难一些。USACO竞赛每一场考试考试都是有四天时间,学生可以在任意一天的当中的任意时间登陆进行时长为四小时的比赛。每一个选手的参赛时间是不同的,靠诚信约束选手不在比赛期间进行交流。
USACO晋级路径
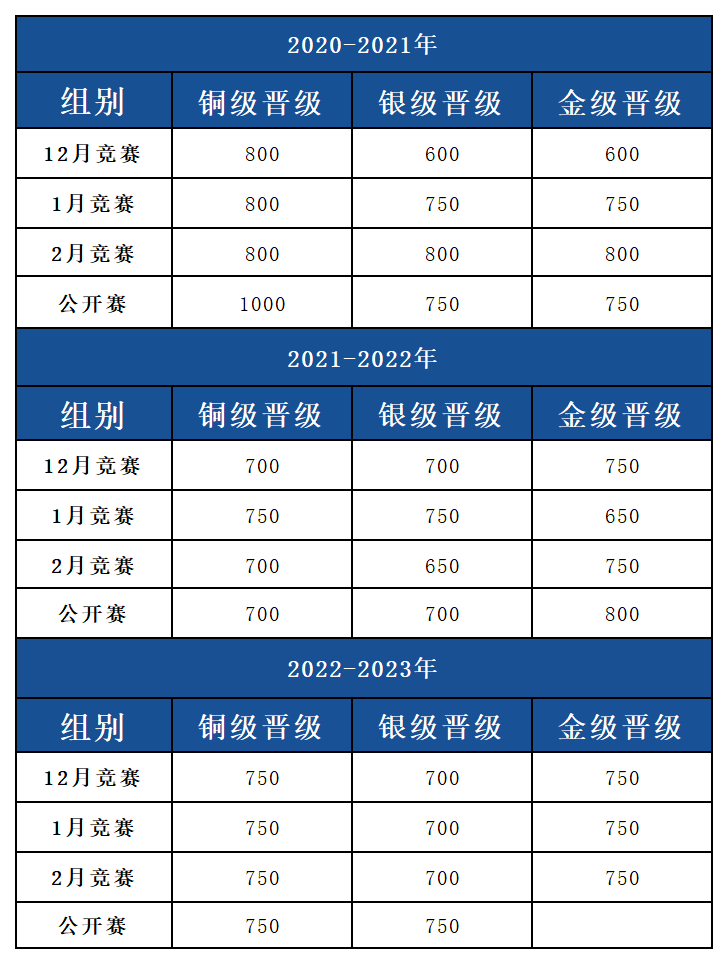
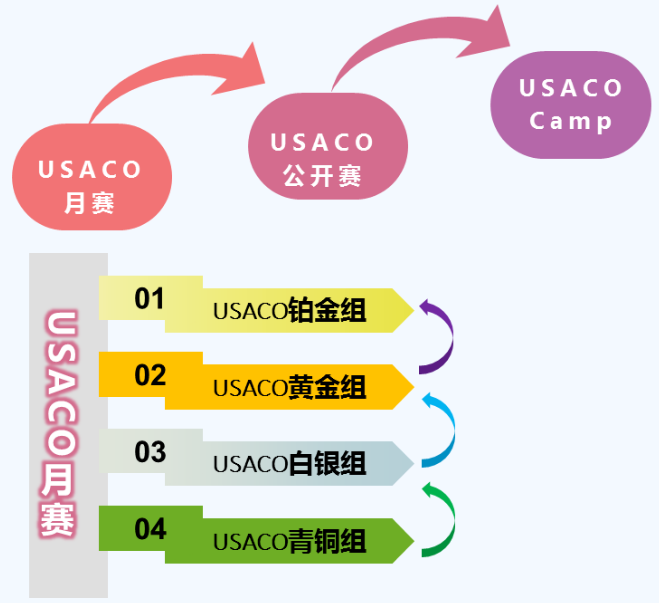
在USACO竞赛中,学生需要逐级晋级,从青铜级别开始,往上逐级挑战,不能跳级参加。但是,如果在考试中取得满分,学生可以直接晋级到下一级别的考试,这为优秀的学生提供了更快的晋级通道。
与国内NOI不同的是,USACO竞赛的级别不会掉,也就是说一旦学生晋级到了某个级别,即使在下一次参赛时,仍然可以参加同样的级别考试,无需从头开始。这种安排为学生提供了更加稳定和持续的挑战和成长机会。
USACO竞赛含金量
助力名校申请:
USACO竞赛成绩优秀的学生在申请美国大学时具有很大的优势,尤其是在计算机专业申请中。越来越多的顶尖大学,如麻省理工、斯坦福等,都将USACO竞赛成绩作为录取的重要参考,为学生升入名校提供有力支持。
培养计算思维:
USACO竞赛的题目涉及算法、数据结构、人工智能、机器学习等领域,通过解题,学生可以锻炼编程思维和解决问题的能力,为未来的学习和职业生涯打下基础,培养学生的计算思维和创新能力。
提高综合素质:
参与USACO竞赛需要学生具备扎实的编程基础、广泛的计算机科学知识以及良好的时间管理和压力应对能力。这些素质的提升不仅有助于学生在学术上的发展,也能为其未来的职业生涯做好准备,提高学生的综合素质和竞争力。
USACO长线备考班、冲刺班已开启,扫描文末二维码领取限时优惠及备赛真题资料~
金牌导师&精编讲义“强强联手”